Deformation in Homogeneized and Discrete Models for Hexagonal Lattice

Large Warping in Body Center Cube Lattice

Description

In a microtruss, the assembly of members in a defined configuration controls the macroscopic response of the material. If the characteristic length of its constituent elements is at least 1 order of magnitude smaller than the macroscopic length of the component, then the lattice can be treated as a material with homogenized properties. The cell geometry (especially the topology of the pore) of a lattice governs not only the structural response but also a range of physical properties, such as wave propagation, energy absorption, toughness and diffusivity.

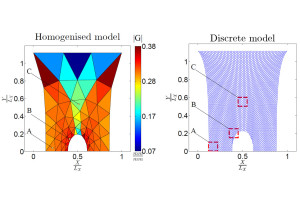
We developed refined constitutive models that can capture the multiscale mechanics of two and three-dimensional lattices with any arbitrary topology, as well as with open and closed cell. Such models enable to treat a lattice component as a homogeneous medium and predict also non-linear structural responses, i.e. deformation mechanisms induced by both geometric and material non-linearity. In particular, we can reproduce phenomena observed during experiments, such as the strain hardening due to the reorientation of the lattice elements, and the structural softening due the microscopic buckling of the struts. We are also contributing to populating the material charts by characterizing the physical properties of new lattices. Besides the modelling, we are working on the design optimization of the lattice microarchitecture for single and multiple functional requirements.

Relevant Publications

• Vigliotti A., Deshpande V. S., Pasini, D., Non linear constitutive models for lattice materials, Journal of the Mechanics and Physics of Solids,  Vol. 64, pp. 44-60, 2014. link to PDF
• Khanoki, S. A., and Pasini, D., Mechanical properties of planar lattice materials via asymptotic homogenization and comparison with alternative homogenization methods, International Journal of Mechanical Science, Vol 77,  pp. 249–262, 2013. link to PDF
• Vigliotti A., Pasini, D., Mechanical properties of hierarchical lattices, Journal of Mechanics of Materials, vol. 62, pp 32-43, 2013. link to PDF
• Vigliotti A., Pasini, D., Stiffness and Strength of Tridimensional Periodic Lattices, Computer Methods in Applied Mechanics and Engineering, Vol. 229-232, pp. 27-43, 2012. link to PDF